微积分笔记 微积分笔记 0

函数

• 反函数与原函数关于 y=x镜面对称

• 函数的复合

[math]f(x)=h(g(x))[/math]可表示为 [math]f=hOg[/math]，即f是g与h的复合。

• 有理函数

[math]f(x)=\frac{p(x)}{q(x)}[/math]

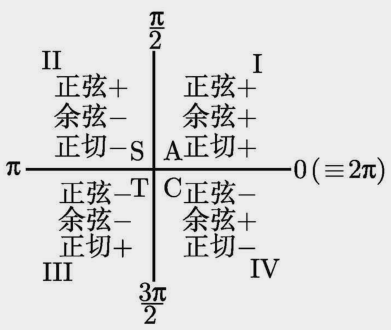
• 三角函数

余割：[math]csc(x)=\frac{1}{sin(x)}[/math]
正割：[math]sec(x)=\frac{1}{cos(x)}[/math]
余切：[math]cot(x)=\frac{1}{tan(x)}[/math]

勾股定理（毕达哥拉斯定理）：

[math]cos^2(x)+sin^2(x)=1[/math]

“互余”：

[math]三角函数(x)=co-三角函数(\frac{\pi}{2}-x)[/math] ，如：

[math]sin(x)=cos(\frac{\pi}{2}-x), sec(x)=csc(\frac{\pi}{2}-x), tan(x)=cot(\frac{\pi}{2}-x)[/math]

其他公式：

[math]sin(A+B)=sin(A)cos(B)+cos(A)sin(B)[/math]

[math]cos(A+B)=cos(A)cos(B)-sin(A)sin(B)[/math]

极限导论

三明治定理(又称作 夹逼定理)：如果一个函数 f 被夹在函数 g 和 h 之间, 当 x → a 时, 这两个函数 g 和 h 都收敛于同一个极限 L, 那么当 x → a 时, f 也收敛于极限 L.

多项式

立方差公式：[math]a^3-b^3=(a-b)(a^2+ab+b^2)[/math]

函数的导数

乘积法则：

[math]如果h(x)=f(x)g(x)，那么h'(x)=f'(x)g(x)+f(x)g'(x)[/math]

[math]如果 y=uvw，那么 \frac{dy}{dx}=\frac{du}{dx}vw + u\frac{dv}{dx}w + uv\frac{dw}{dx}[/math]

商法则：

[math]如果 h(x)=\frac{f(x)}{g(x)}，那么 h'(x)=\frac{f'(x)g(x)-f(x)g'(x)}{(g(x))^2}[/math]

链式求导法则：

[math]如果 h(x)=f(g(x))，那么 h'(x)=f'(g(x))g'(x)[/math]

三角函数

三角函数关键公式：
[math]\lim_{x \to 0}\frac{1-\cos(x)}{x}=0[/math]

[math]\lim_{x \to 0}\frac{\sin(x)}{x}=1[/math]

指数函数和对数函数

如果[math]N=a^x[/math]，即a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作[math]x=\log_{a}N[/math]。其中，a叫做对数的底数，N叫做真数，x叫做“以a为底N的对数”。

1. 特别地，我们称以10为底的对数叫做常用对数（common logarithm），并记为lg。
2. 称以无理数e（e=2.71828...）为底的对数称为自然对数（natural logarithm），并记为ln。
3. 零没有对数。
4. 在实数范围内，负数无对数； 在复数范围内，负数是有对数的。

对数法则

...略
[math]\log_{b}(x^y)=ylog_{b}(x)[/math]
[math]\log_b(x)=\frac{\log_c(x)}{\log_b(c)}[/math]

复利极限

令 [math]e = \lim_{h \to 0+}(1+h)^{1/h}[/math](e=2.718...)，则：

[math]\lim_{n \to \infty}(1+\frac{x}{n})^n=e^x[/math] 和 [math]\lim_{h \to 0}(1+xh)^{1/h}=e^x[/math]

导数

[math]\frac{d}{dx}\log_{b}(x)=\frac{1} {xln(b)}[/math] 和 [math]\frac{d}{dx}(b^x)=b^xln(b)[/math]

指数增长/衰减方程

[math]P(t)=P_0e^kt[/math]，k为增长/衰减常数，k>0时为增长方程，相应地，k<0为衰减方程。

双曲函数

定义：

[math]cosh(x)=\frac{e^x+e^{-x}} {2}, sinh(x)=\frac{e^x-e^{-x}} {2}[/math]

有：

[math]cosh^2(x)-sinh^2(x)=1[/math]

[math]\frac{d}{dx}sinh(x)=cosh(x)[/math]

[math]\frac{d}{dx}cosh(x)=sinh(x)[/math]

曲线：

最优化和线性化

线性化

对于函数 [math]f[/math] 在 [math]x[/math] 上的值 [math]f(x)[/math]，可以选取一个接近于 [math]x[/math] 的 [math]a[/math](使得 [math]f(a)[/math]可以轻易计算)，再对 [math]f[/math]求导得出 [math]f'(x)[/math]，则可利用线性化计算出 [math]f(x)[/math]：
[math]f(x) \approx L(x)=f(a)+f'(a)(x-a)[/math]

误差方程：

[math]r(x)=f(x)-L(x)=\frac{1}{2}f''(c)(x-a)^2[/math]

取绝对值：

[math]|误差|=\frac{1}{2}|f''(c)||x-a|^2[/math]

对 [math]|f''(c)|[/math]取最大值 M：

[math]|误差|\le\frac{1}{2}M|x-a|^2[/math]

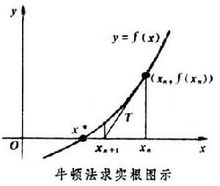
牛顿法

对于某些函数 [math]f(x)[/math]，我们想取其与 [math]x[/math]轴交点，即 [math]f(x)=0[/math]时对应的 [math]x[/math]，直接计算非常困难，我们则可以尝试用牛顿法逼近：

我们先取任意一点，如 [math]x_n[/math]，然后计算出对应的 [math]f(x_n)[/math]，然后应用线性化模拟 [math]f(x)[/math]，取出对应线性函数与 [math]x[/math]轴交点，有：

[math]f(x_n)+(x_{n+1}-x_n)f'(x_n)=0[/math]

这样我们可以得到 [math]x_{n+1} = xn - \frac{f(x_n)}{f'(xn)}[/math]

一般情况下，[math]x_{n+1}[/math] 对应的 [math]f(x_{n+1})[/math] 是比 [math]f(x_n)[/math]更接近于 0的，如此迭代，则能无限逼近 [math]f(x)=0[/math]的解 [math]x[/math].

洛必达法则

如果[math]f(a)=g(a)=0[/math]，则有 [math]\lim_{x \to a} \frac {f(x)}{g(x)} = \lim_{x \to a} \frac {f'(x)}{g'(x)}[/math]，假设等式右边的极限存在。

积分

求[math]\sum_{j=a}^b j[/math]的值：

我们知道 [math]\sum_{j=a}^b j[/math] = [math]\sum_{j=a}^b (b-j+a)[/math]，我们令其和为 S，则：

[math]\sum_{j=a}^b j + \sum_{j=a}^b (b-j+a) = 2S[/math]，而

[math]\sum_{j=a}^b j + \sum_{j=a}^b (b-j+a) = a+b+(a+1)+(b-1)+...+j+(b-j+a)+...+b+a=\sum_{j=a}^b(a+b)=(a+b)(b-a)=2S[/math]，即：

[math]\sum_{j=a}^b j=\frac{(a+b)(a-b)}{2}[/math]

伸缩求和法

求[math]\sum_{j=1}^n(j^2-(j-1)^2)[/math]的值：

[math]\sum_{j=1}^n(j^2-(j-1)^2)=(1^2-0^2)+(2^2-1^2)+(3^2-2^2)+...+(n^2-(n-1)^2)=n^2-0^2[/math]

这样的级数我们称为伸缩级数，有：

[math]\sum_{j=a}^b(f(j)-f(j-1)) = f(b) - f(a-1) [/math]

同样，对于 [math]\sum_{j=1}^n(j^2-(j-1)^2)[/math]，我们将 [math](j^2-(j-1)^2)[/math]进行分解，得到[math]2j-1[/math]：

[math]\sum_{j=1}^n(j^2-(j-1)^2) = \sum_{j=1}^n(2j-1) = 2\sum_{j=1}^{n}j-n[/math]，代入伸缩级数求和的值 [math]n^2-0^2[/math]，可以同样得出：

[math]\sum_{j=1}^{n}j = \frac{n^2-0^2+n}{2}=\frac{(n+1)n)}{2}[/math]

类似地，可以得出：

[math]\sum_{j=1}^{n}j^2 = \frac{n(n+1)(2n+1))}{2}[/math]

微积分

令[math]F(x)= \int_{a}^xf(t)dt[/math]，有：

微积分第一基本定理：

[math]F'(x)=\frac{d}{dx}\int_{a}^xf(t)dt=f(x)[/math]

• 如此，在计算 [math]\int_{a}^xf(t)dt[/math]时，由于 [math]F(x)= \int_{a}^xf(t)dt[/math]，我们只要求出对应的 [math]F(x)[/math]即可，而 [math]F'(x)=f(x)[/math]，故只要思考得到什么函数的导数是[math]f(x)[/math]，则可得到 [math]F(x)=G(x)+C[/math]，再代入[math]F(a)=G(a)+C=0[/math]即可求出常量 [math]C[/math]。

微积分第二基本定理：

[math]\int_{a}^bf(t)d(t)=F(b)-F(a)[/math]

不定积分

[math]∫f(x)d(x)[/math]表示函数[math]f(x)[/math]的反导数集合，如果 [math]\frac{d}{dx}F(x)=f(x)[/math]，则：

[math]∫f(x)d(x) = F(x) + C[/math]

分部积分法

[math]∫udv = uv - ∫vdu[/math]

反常积分

定义

如果出现下面三种情况，积分 [math]\int_{a}^bf(x)dx[/math]就是反常积分：

1. 函数[math]f(x)[/math]在 [math][a, b][/math]内是无界的
2. [math]a=\infty[/math]
3. [math]b=-\infty[/math]

收敛or发散

如果仅仅在 x接近于 a点该函数 f(x)是无界的，则定义：

[math]\int_{a}^bf(x)dx=\lim_{\varepsilon \to 0}\int_{a+\varepsilon}^bf(x)dx[/math]

如果积分存在，我们说这个反常积分收敛，否则则为发散。

无穷区间上的积分

[math]\int_{a}^\infty f(x)dx = \lim_{N \to \infty}\int_{a}^N f(x)dx[/math]

[math]\int_{-\infty}^b f(x)dx = \lim_{N \to -\infty}\int_{N}^b f(x)dx[/math]

极限比较判别法

如果 [math]\lim_{x \to a} \frac{f(x)}{g(x)}=1[/math]，我们说当 [math]a \to b[/math]时，[math]f(x)[/math] 和 [math]g(x)[/math] 是渐近等价的，即 [math]f(x) \sim g(x)[/math]。

极限比较判别法 定义：

如果 [math]a \to b[/math]时 [math]f(x) \sim g(x)[/math]，且这两个函数 [a,b]上没有其他瑕点了，那么积分 [math]\int_{a}^b f(x)dx[/math] 与 [math]\int_{a}^b g(x)dx[/math]是同时收敛或同时发散的。

p判别法

• [math]\int_{}^\infty [/math]的情况：对于任何有限值 [math]a \gt 0[/math]，积分 [math]\int_{a}^\infty \frac{1}{x^p}dx[/math]，在 [math]p\gt 1[/math] 时是收敛的，在 [math]p\le1[/math]时是发散的。
• [math]\int_{0}[/math]的情况：对于任何有限值 [math]a \gt 0[/math]，积分 [math]\int_{0}^a \frac{1}{x^p}dx[/math]，在 [math]p\lt 1[/math] 时是收敛的，在 [math]p\ge1[/math]时是发散的。

绝对收敛判别法

如果[math]\int_{a}^b|f(x)|dx[/math]是收敛的，那么 [math]\int_{a}^bf(x)dx[/math]也是收敛的。

复数

欧拉公式

[math]x+iy=re^{iθ}[/math]